Software Case Study: Oil and Gas Development and Production
The case was provided by Steve Hoye. Steve is an independent business consultant with 23 years of experience in the oil and gas industry, specializing in Monte Carlo simulations for the oil and gas industry. After earning a Bachelor of Science degree from Purdue University in 1980, he worked as a geophysicist for Texaco in Houston, Denver, and Midland, Texas, until he received an MBA from the University of Denver in 1997. Since then, he has been a leader in Texaco, the leader of the BU technology group in the Central Plains, and the manager of the Texaco Permian Basin business unit asset group, which began his consulting business in 2002.
The oil and gas industry is a good place to test and discuss risk analysis techniques. The basic business model we discussed involved land rights, geological data, drilling (services and hardware) and expert investments, and in return we would get an oil or gas production line and sell oil and gas to make a profit. The model is surrounded by diverse and prominent risk factors that determine the probability of success of the project, including:
Dry well risk. Since no oil or natural gas was found in the geological formations that were drilled, there was no gain in the dollar invested in drilling. Drilling risk. High drilling costs often undermine the profitability of the project. Although the company makes every effort to accurately estimate it, unpredictable geological and mechanical difficulties can cause significant changes in actual costs. Production risk. Even though reservoirs and gas reservoirs have been discovered through drilling, the possibility of miscalculation of oil and gas scale and recoverability is also high. Price risk. The oil and gas industry is cyclical, and in many major political events, product prices can change unexpectedly, such as the Middle East war, OPEC cartel overproduction and fraud, supply disruptions, large refinery fires, worker strikes, or high yields. Political unrest in oil countries (such as Venezuela in 2002) and changes in world demand. Political risk. A large number of oil and gas reserves in the world are controlled by unstable governments. Companies with investment projects in these countries bear huge risks because when they should share their income according to the contract, the government or leader who signs the contract with the company may no longer be in power. In many documented cases, the company's investments in land, factories, and equipment were simply nationalized by local governments, leaving no revenue to the company or leaving only the equipment and facilities they built to earn revenue.The oil and gas industry is generally highly capital intensive, and usually the risk is not just interest. When allocating capital budgets in a way that seeks to ensure the value of the stock, business units and the entire enterprise are betting on their ability to estimate these risks accurately. To emphasize the importance of industry risk management, many large oil companies have authorized senior company expert teams to review the risk assessments of all business units in large projects. These reviews attempt to ensure the authenticity of risk assessments between different departments and divisions, as departments and divisions always try to make the company's leadership feel that their portfolio is attractive when competing for capital.
Monte Carlo simulation is a preferred method for evaluating a model with multiple complex risk factors. Due to the inherent complexity of these risk factors and their interactions, the identified solutions are not realistic, and the use of point estimates is limited and may even be misleading. In comparison, Monte Carlo simulation is the ideal method for economic evaluation in these situations. Experts in one area can separately quantify and account for project risks associated with their area of ​​expertise without having to detail the economic impact of these risks on the entire project. For each commissioned expert, the cash flow model that integrates the risk diversification hypothesis is relatively straightforward to construct and analyze. Most importantly, the resulting predictions are not simply a single point estimate of the probability of an oil and gas exploration. Instead, they provide management with a range of possible outcomes and corresponding probabilities. Best of all, Monte Carlo simulations provide an estimate of the sensitivity of the investment results to key assumptions in the model, which allows them to focus their funding and workforce on key factors that will determine whether they can be specified in the business plan. Financial goals. Ultimately, Monte Carlo simulation is a project management tool that reduces risk and increases profits.
In this case study, we will study an example of oil drilling exploration. And take into account many of the aforementioned risks. Because the model is hypothesized, the general parameters we use are consistent with the parameters of drilling in mature oil-rich basins in the United States (for example, the Permian basin in West Texas), and these parameters are expressed using risk factors and their income expenditures. . This model is more like a basic framework and method than an assessment of a drilling survey. Its value lies in the method of using Monte Carlo simulation to quantify important risk assumptions in oil exploration and to analyze its impact on project prediction probability. The techniques described here can be extended to other different types of oil and gas exploration.
Cash flow model
This model was created to provide all the required Monte Carlo simulation tools, which are easy-to-use, comprehensive add-ons in Excel. Using the dry well risk factor for a particular geological formation and basin, the model simulates the drilling result as a dry or oil well. Whether the well is a dry or oil well, drilling, earthquake and land lease costs will exist. If the well is an oil well, the income stream is calculated based on the assumed oil price and the decreasing oil production rate over time. Some of the costs will be deducted, that is, the landlord’s patent fees, the operating costs of the oil production process, and the state government’s severance tax on oil production. Finally, these net cash flows are discounted according to the company's capital-weighted cost (WACC) and added to the project's net present value (NPV). Now let's discuss each model part in more detail.
Dry well risk
For the risk of not finding any oil and gas in the well, companies generally have a proprietary plan to quantify. In general, four independent basic conditions must be met in order for the drill to find oil and gas resources:
(1) Oil and gas must exist.
(2) A container must be formed in the rock formation to store these oil and gas.
(3) An impermeable seal layer must be provided to secure the oil and gas in the vessel to prevent it from migrating to other locations.
(4) There must be a structure or closure to concentrate the oil and gas at the point where the drill bit penetrates.
Because these four conditions are independent of each other and each condition must be established in order for the drill bit to drill into oil and gas (avoiding dry wells), the probability of an oil well is defined as:
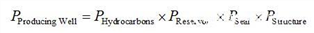
Figure 1.1 shows a part of the model called “Dry Drilling Risk†and the Monte Carlo hypothesis probability distribution for each factor. A project team often describes each factor as a single point estimate, and sometimes we use other methods to quantify these risks. The most effective method is for the exploration team to show geological, geophysical and engineering factors to experts who have extensive experience in a particular field. These peer experts then rate the risk factors. The resulting risk factor distribution often exhibits an approximately normal distribution with a strong central tendency and a symmetric two-tailed. This method is able to withstand the Monte Carlo simulation test. It highlights the factors that have a general consensus on the risks it will bring, placing the most risky factors on the table and conducting research and special treatment.

Figure 1.1 Dry drilling risk (partial)
The assumptions about dry well risk in the model reflect a relatively low risk profile. Each of the four risk factor assumptions in Figure 1.1 (black shaded area) is described as a normal distribution variable, with the mean and standard deviation of each distribution to the right of the hypothetical area. The range of these normal distributions is limited and truncated between the minimum and maximum values, and any random sampling of simulations outside this interval is ignored and considered unrealistic.
As mentioned earlier, the net success probability area of ​​the production well in the model is equal to the product of the aforementioned four risk factors. In each trial or cycle in the simulation, four risk factors were randomly sampled from their respective normal distributions. Finally, during each cycle of the Monte Carlo simulation, the area labeled Production Well produces a random number between 0 and 1 to determine whether the simulation found oil or just a dry well. If the random number is less than the net success probability of the production well, then he is the production well and displays the number 1. Conversely, if the random number is greater than the net success probability of the production well, the simulated well is a dry well and displays zero.
Production risk
A multi-year oil flow can be described by the initial oil recovery rate (measured by how many barrels of oil per day, BOPD) and the rate of oil recovery, as natural reservoirs and volumes are decreasing year by year. Reservoir engineers can use many mathematical models to describe production declines, and it is best to choose the ones that best match geology to describe the reservoir. Our hypothetical oil flow production is described by the following two parameters:
1. IP. The initial oil recovery rate measured from drilling.
2. Declining rate. This is an exponentially decreasing productivity that describes the annual production reduction from the beginning of the year to the end of the year. The productivity calculation formula expressed by BOPD in our model is:
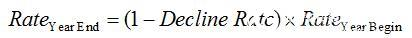
The annual production of oil barrels is approximately:
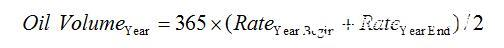
In Monte Carlo simulations, our model describes IPs as mean 441 BOPD with a standard deviation of 165 BOPD lognormal distribution. The rate of decline is evenly distributed between 15% and 28%. To give our hypothetical model some fun and realism, we add an additional constraint to the production model to simulate a situation that may occur in a particular reservoir, and high IPs in the reservoir means a high production decline rate. This constraint is to add a correlation coefficient of 0.6 between the IP and the declining rate randomly extracted from the respective distributions in each simulation test.
The production and operating costs of the model are shown in Figure 1.12. Although only the first three years of data are shown, the model illustrates 25 years of production. However, when production falls to the economic boundary, the year and subsequent annual costs are zero, ending the production life of the well. As shown in Figure 1.12, IP is generated at the end of the year 0 and is divided by the output value of the first year at the end of the first year.
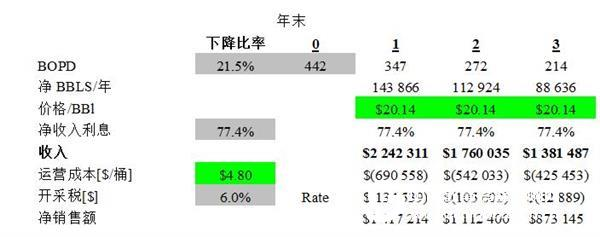
Figure 1.2 Production and operation costs (partial)
Income section
Model revenue is literally derived from previously calculated oil sales. Two assumptions are used in our model to describe exploration risks:
1. price. In the past 10 years, oil prices have risen from $13.63 per barrel in 1998 to $30 per barrel in 2000. To be consistent with these data, our model assumes that the oil price is subject to a mean distribution of $20.14 per barrel and a standard deviation of $4.43 per barrel.
2. Net income benefits. Oil companies must purchase lease rights from holders of mineral interests. While paying cash to maintain mining and production rights for a specific period of time, the lessee generally retains a percentage of the oil production income as a rental fee. The percentage of the production company that has been retained after paying all the rental fees is the net income benefit (NRI). Our model describes a typical West Texas case and assumes that the NRI follows a normal distribution with a mean of 75% and a standard deviation of 2%.
Figure 1.12 also shows the revenue portion of the model, just below the production stream.
Operating expenses section
Below the income section is the running expenses section, which includes two assumptions:
1. Operating costs. Companies must pay for the labor and hardware facilities in the production process. These costs are often expressed in dollars per barrel. A reasonable West Texas cost would be $4.8/barrel with a standard deviation of .60/barrel.
2. Dismissal tax. The state government's tax on the oil and gas produced is assumed to be a fixed value, which is 6% of income.
The total sales minus the operating expenses yields net sales, as shown in Figure 1.2.
The cost of year 0 Figure 1.3 shows the cost for year 0, which is assumed to occur before oil is recovered from the well (with income). These fees include:
1. Drilling costs. As mentioned earlier, these costs can vary drastically due to geological, engineering and mechanical uncertainties. It is also reasonable for us to skew the drilling cost distribution because it explains the high-end tail of a few wellheads that contain high drilling costs, which are caused by mechanical failures and unforeseen geological conditions or emergencies. Therefore, our distribution is assumed to be a logarithmic distribution with a mean of $1200000 and a standard deviation of $200000.
2. Completion costs. If it is determined that there is oil in the reservoir (we did not drill dry wells), the engineer must prepare (both mechanical and chemical) for oil extraction at an optimal sustainable rate. For this particular well, we assume that the engineer believes that the cost is subject to a normal distribution of $287,000 and a standard deviation of $30000.
3. Professional total expenses. The project team's annual salary and allowance costs are $320000, and we believe that they spend the most time in a triangle, with a maximum likelihood ratio of 50%, a minimum of 40%, and a maximum of 65%.
4. Earthquake and rental costs. To develop this program, our team needed to purchase seismic data to select the best wellhead location and to purchase the right to drill on many of the land near the wellhead. Since the well is not the only wellhead based on these seismic data and land, these costs are allocated to all wellheads planned in the project. Uncertainty assumptions are shown in Figure 1.4, including the number of acres rented, and we assume that it is subject to a normal distribution of 12,000 acres with a standard deviation of 1,000 acres. The total number of wellheads participating in the cost allocation is assumed to be a uniform distribution of 10 to 30. We assume that the area of ​​the seismic data is subject to a normal distribution with a mean of 50 square miles and a standard deviation of 7 square miles. These costs are shown in the last two lines of Figure 1.3.

Net present value part
The last part of the model adds the annual income and expenditures starting in year 0 and discounts them according to the capital-weighted cost (WACC – we assume 9% in this model), and then adds the discounted values ​​for each year. Calculate the NPV prediction for this project. In addition, calculate NPV/I, which can be used as a threshold and ranking mechanism in portfolio decisions when the firm determines whether the project meets other investment opportunities under a limited capital budget.
Monte Carlo simulation results
After a predetermined hypothesis, when we estimate the results of the simulation run, it is useful to define and compare a single point estimate of the project value, which is calculated using the mean or maximum likelihood of the model hypothesis. The expected value of the project is defined as:
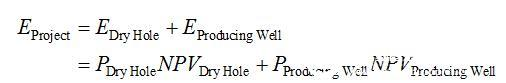
Among them: Pproducting Well = probability of producing oil well, PDryHole = probability of dry well = (1- Pproducting Well). Projects with a mean or maximum likelihood value in the model expect an NPV of $1250000, which may be an attractive expectation in a company's portfolio.
In contrast, we can now test this series of results and their probability of occurrence. In the simulation, 8450 tests (determination of the number of trials by precision control) were performed to predict NPV, and a 95% confidence interval was obtained with a mean value of ±$50000. Figure 1.5 is a frequency distribution diagram of the NPV results. This distribution is clearly bimodal, with the larger NPV spikes on the left side of the graph representing the results of the dry well. The smaller and wider kurtosis is oriented towards the high NPV value, which represents the positive NPV value associated with the production well and is also broader.
In Figure 1.5, all negative NPV values ​​are on the left side of the NPV=0 line (light shade), while the positive NPV value is on the right side of the line, and the probability of a positive result (flat or better) is shown as 69.33 %. We are interested in the fact that the probability of a negative result includes not only the portion of the dry well shown, but also a small portion of the apparent production well that will also cause the company to lose money. From this information we can conclude that the probability of a negative NPV for the project is 30.67%.
For this type of project, it is not good enough to just avoid negative NPV values. A project must provide shareholders with a higher return than the cost of capital. Further, the project must be competitive compared to other investment opportunities owned by the company. If we assume that the company's annual budget has a minimum expected return rate of NPV/I greater than 25%, then we will test whether our simulated project results exceed the minimum expected rate of return.
Figure 1.6 shows the distribution of predicted results for NPV/I. The large kurtosis at -100% also represents the case of a dry well. In fact, the NPV value here is the negative of the 0th year cost, making NPV/I equal to -1. It can be seen from the figure that the probability of a project NPV value greater than 25% is 64%. In the risk-sensitivity system, this result means that the probability that the project NPV is lower than the company's minimum expected rate of return is greater than 1/3 – it is indeed a higher risk.

Finally, we can also study the sensitivity of project results to risks and assumptions. Figure 1.7 shows the sensitivity analysis of the project NPV values ​​to the assumptions made in the model. This graph shows the correlation coefficients of the top 10 model hypotheses and NPV predictions, and is arranged in descending order.
At this point, the project manager can focus resources on factors that have an impact on the probability of the project. With the information in Figure 1.7, we can assume the top few risks in the project and rank them by importance:

Figure 1.7 Sensitivity analysis
Initial oil recovery rate (IP). The initial oil recovery rate of the oil well has a driving effect on the project value, and the uncertainty of the ratio prediction leads to the maximum fluctuation of the project prediction result. Therefore, we can allow our reservoir team and production engineers to further study the production IP values ​​of similar reservoirs in the region, or try to stratify the data based on drilling or completion techniques, geological factors and geophysical data. To further improve IP prediction. Reservoir risk. This assumption affects whether a wellhead is a dry well or a production well, so it is not surprising to say that it is a major driver. Insufficient analysis of underground rock data will lead the company to declare a wellhead with mining potential as a dry well, and the project team can investigate the probability of this happening in many ways. Oil price (first year) and drilling costs. These two have a close relationship in the efficacy of NPV. The best way to deal with price uncertainty is to determine a standard forecast price so that the company can compare all items. Drilling costs can be minimized by the process, which leads to the gap between small forecasted costs and actual costs. Companies can find records of other companies in reliable, low-cost drilling projects. Declining rate. Careful readers will find a positive correlation between the rate of decline and the project NPV. At first glance, it feels a bit unexpected, because we usually think that a higher rate of decline will reduce oil sales and affect project revenue. However, recall that we interpolate the high IPs value with the high declining rate in the model hypothesis, which indirectly illustrates the effect of IP on the project NPV: although the rate of decline is higher, the positive impact of IP on the project value is faster than that of the reservoir. The loss of production due to decrement. We must double our efforts to better predict the IP in the model.in conclusion
When evaluating oil and gas exploration under very uncertain complex conditions, Monte Carlo simulation can be an ideal tool if the single point estimate of the project results is almost ineffective. The technology provides a straightforward and effective way for each member of a multidisciplinary team to quantify and account for the risk factors each team member believes has an impact on the drilling project. In addition, Monte Carlo simulation provides management and team leaders with something more valuable than project NPV predictions: it provides a probabilistic distribution of the results of a whole series of projects, at which point decision makers can explore any value related to the project. Other circumstances. These situations may include the probability of a break-even, a project result that may undermine the project team's reputation and thus may not be capitalized in the future, or a very successful project outcome. Finally, the Monte Carlo simulation of oil and gas exploration provides managers and team leaders with the key message of which risk factors and assumptions contribute to the increased probability of project outcomes, and they will receive all these important feedbacks. Human and financial resources are concentrated on these risk assumptions that have the greatest positive impact on the project, which can increase their efficiency and increase profits.
X-Type Tripod Screen,Portable Projector,Outdoor Projector Screen,Portable Projector Screen Tripo
Dongguan Aoxing Audio Visual Equipment CO.,Ltd , https://www.aoxing-projectorscreen.com